Life is a set of choices.  Lets simplistically boil this down to two choices: Work and Play. The return you get by investing energy in a particular choice vs energy invested in that choice is plotted. X is energy invested. Y is return. 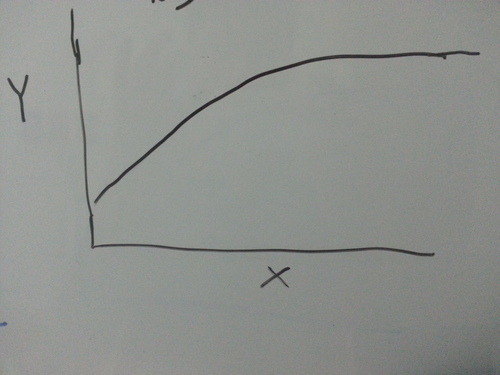X and Y have different meaning in different contexts. In context of work (for example studies), the graph would show the marks vs hours spent studying. When you’re studying very little, any increase in time spent study delivers a pretty high gain in terms of Y (left side of graph) . However, if you’re already spending a whole lot of time studying, increasing your efforts produces a marginal increase in marks (right side of graph) . The assumption is that hours spent studying singly and directly affects marks, please bear with me.

Similarly you can interpret the above graph in the the context of play/fun too. It gives you a lot of enjoyment of skip an hour of work and catch up on that TV show, but watch 10 hours of TV non-stop and the enjoyment you get is certainly not 10 times what you got out of spending one hour with the television . Here too, enjoyment derived saturates with energy invested.

Walking further down the road. Lets call energy spent in work W and energy spent in play P. You have finite energy so, W+P=1 (I call it 1 but it’s just some constant).  The graph i described is basically that of the log function so: Enjoyment(E) = log(T) where T ϵ {W,P} The rest of the derivation can be followed along in the picture above. Final result: Net enjoyment (E) = log x*(1-x) + c where x is fraction of energy spent in work.  The plot of E peaks at x=0.5 i.e. when x=1-x or when energy spent in work equals energy spent in play.  Voila! Hence proved that work-life balance is crucial to your happiness; also proves that money can’t buy happiness?  Next steps, complicate the equation and factor in temporality.