Look at the figure below and try to draw it , the condition is that you cannot lift your pen from the paper i.e. you have to draw it in one stroke and you cannot go over any edge more than once i.e. tracing out a line you’ve already drawn.
If you are seeing this for the first time , try drawing it for at least 5 minutes before you read the rest of this post.

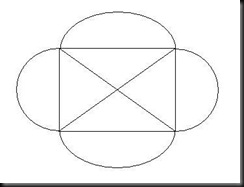
Well , many  times from my childhood to now people have challenged me to draw this figure. This problem bugged me for a really long time because i always believed there was a way to do it ; well guess what , there isn’t.
Most people cheat and draw the figure by folding the page and moving the pen around or by drawing it really fast so you cant see it when they cover an edge twice.You can try and try but you will have no success whatsoever because this figure is simply impossible to draw.I’m not saying that  because I’ve failed like a zillion times but because i can mathematically prove it.
I found the answer to the question of whether this figure could be drawn or not when i was reading up on Euler and came  across The Königsberg Problem which he had solved. Seeing the solution I realized that the theory could help me find an answer to the above question.
The Proof (Using Graph Theory):
To be able to draw to the figure in one go , you must traverse every edge one and only time.
Graphs on which such an operation can be performed are called Eulerian Paths.
The condition for a graph to be an Eulerian path is that it must have atmost two vertices of odd degree.
Now as we can simply observe , the vertices of the square in the middle are all odd in degree(i.e. they have an odd no. of lines/graph edges touching them).
That makes four odd vertices which violates the condition for an Eulerian path.
Hooray!